Word Search

Problem

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example 1:

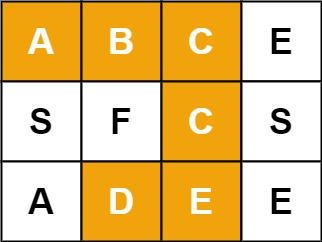
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true

Example 2:

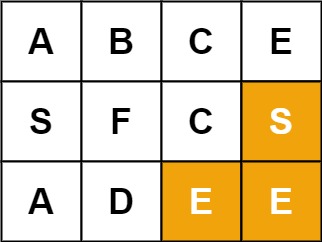
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true

Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false

Constraints:

m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board and word consists of only lowercase and uppercase English letters.

Solution

/**
 * @param {character[][]} board
 * @param {string} word
 * @return {boolean}
 */
var exist = function(board, word) {
    for (let i = 0; i < board.length; i++) {
        for (let j = 0; j < board[i].length; j++) {
            if (dfs(board, word, i, j, 0)) {
                return true;
            }
        }
    }
    return false;
};

var dfs = function(board, word, row, col, index) {
    // (row, rol) is not out of range, has not been used, and current cell matches character of word
    if (board?.[row]?.[col] === word[index]) {
        board[row][col] = null;
        const found = index === word.length - 1 ||
            dfs(board, word, row + 1, col, index + 1) ||
            dfs(board, word, row - 1, col, index + 1) ||
            dfs(board, word, row, col + 1, index + 1) ||
            dfs(board, word, row, col - 1, index + 1)
        board[row][col] = word[index];
        return found;
    }
    return false;
};

We will implement a DFS solution. We iterate through all cells of board and apply DFS method dfs at (i, j), while also keeping track of the current index of word that needs to be matched. Once we reach the last index such that it matches word (ie. board[row][col] == word[index] && index == word.length - 1), then we know word must exist in board. In addition, to prevent re-using the same letter cell, set the cell to null before making any recursive calls (and revert it back before returning).

Problem​

Solution​

Problem

Solution