Search a 2D Matrix II
Problem
Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:
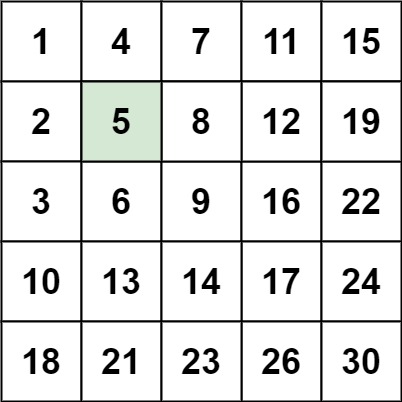
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 Output: true
Example 2:
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- All the integers in each row are sorted in ascending order.
- All the integers in each column are sorted in ascending order.
-109 <= target <= 109
Solution
/**
* @param {number[][]} matrix
* @param {number} target
* @return {boolean}
*/
var searchMatrix = function(matrix, target) {
const m = matrix.length;
const n = matrix[0].length;
let r = 0;
let c = n - 1;
while (c >= 0 && r < m) {
if (target < matrix[r][c]) {
c--;
} else if (target > matrix[r][c]) {
r++;
} else {
return true;
}
}
return false;
};
Observe that matrix has a similar property to a BST. More specifically, given any value at matrix[i][j], the value matrix[i + 1][j] is greater, and the value matrix[i][j - 1] is smaller. In some sense, these two values can be thought of as the left and right nodes of a BST. Thus, the root of the tree would correspond to the top right corner of matrix. Starting from the root, we traverse the matrix by moving either left or down until finding target or going out of range.