All Nodes Distance K in Binary Tree

Problem

Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.

You can return the answer in any order.

Example 1:

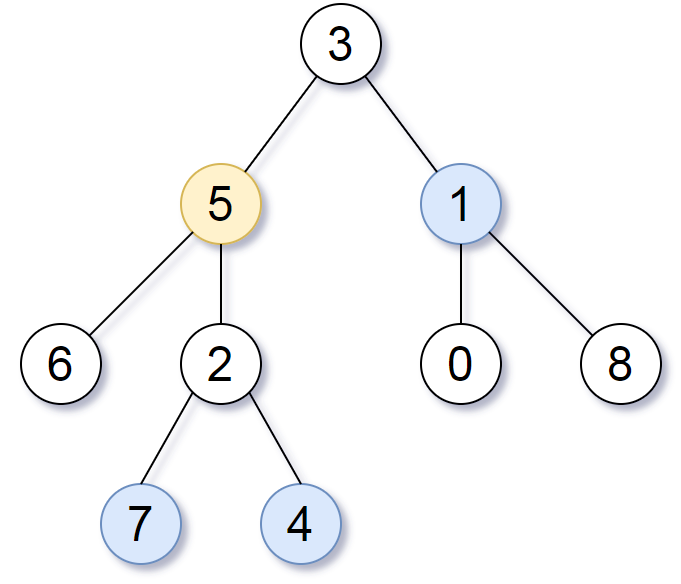
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
Output: [7,4,1]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.

Example 2:

Input: root = [1], target = 1, k = 3
Output: []

Constraints:

The number of nodes in the tree is in the range [1, 500].
0 <= Node.val <= 500
All the values Node.val are unique.
target is the value of one of the nodes in the tree.
0 <= k <= 1000

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} target
 * @param {number} k
 * @return {number[]}
 */
var distanceK = function(root, target, k) {
    // generate undirected graph from node (DFS)
    const graph = [];
    const generateGraph = (node, parent) => {
        if (!node) {
            return;
        }
        while (!graph[node.val]) {
            graph.push([]);
        }
        if (parent) {
            graph[node.val].push(parent.val);
            graph[parent.val].push(node.val);
        }
        generateGraph(node.left, node);
        generateGraph(node.right, node);
    }
    generateGraph(root, null);

    // find kth level nodes using target as root (BFS)
    const queue = [target.val];
    const visited = [];

    for (let level = 0; level < k && queue.length; level++) {
        const n = queue.length;

        for (let i = 0; i < n; i++) {
            const u = queue.shift();
            visited[u] = true;

            for (const v of graph[u]) {
                if (!visited[v]) {
                    queue.push(v);
                }
            }
        }
    }
    return queue;
};

We will implement a BFS and DFS solution. We first create an adjacency undirected graph graph of the tree root with DFS. Using graph, we can simply do a level order traversal with BFS and return all nodes that are on the kth level.

Problem​

Solution​

Problem

Solution