Kth Smallest Element in a Sorted Matrix

Problem

Given an n x n matrix where each of the rows and columns is sorted in ascending order, return the kth smallest element in the matrix.

Note that it is the kth smallest element in the sorted order, not the kth distinct element.

You must find a solution with a memory complexity better than O(n2).

 

Example 1:

Input: matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
Output: 13
Explanation: The elements in the matrix are [1,5,9,10,11,12,13,13,15], and the 8th smallest number is 13

Example 2:

Input: matrix = [[-5]], k = 1
Output: -5

 

Constraints:

• n == matrix.length == matrix[i].length
• 1 <= n <= 300
• -109 <= matrix[i][j] <= 109
• All the rows and columns of matrix are guaranteed to be sorted in non-decreasing order.
• 1 <= k <= n2

Solution

/**
 * @param {number[][]} matrix
 * @param {number} k
 * @return {number}
 */
var kthSmallest = function(matrix, k) {
    const minHeap = new MinPriorityQueue({ priority: tuple => tuple.val });
    const n = matrix.length;
    let res = 0;

    // push first col into heap
    for (let i = 0; i < n; i++) {
        minHeap.enqueue({ r: i, c: 0, val: matrix[i][0] });
    }

    // find kth smallest element
    for (let i = 0; i < k; i++) {
        const t = minHeap.dequeue().element;
        res = t.val;
        if (t.c + 1 < n) {
            minHeap.enqueue({ r: t.r, c: t.c + 1, val: matrix[t.r][t.c + 1] });
        }
    }
    return res;
};

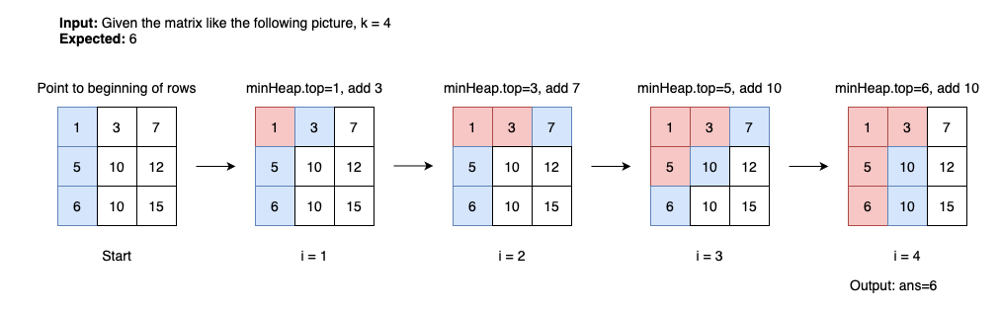
The solution is extremely similar to Merge k Sorted Lists. We can either use the rows or cols as n sorted lists to find the kth smallest element.

Follow-up

Could you solve the problem with a constant memory (i.e., O(1) memory complexity)?

Solution

/**
 * @param {number[][]} matrix
 * @param {number} k
 * @return {number}
 */
var kthSmallest = function(matrix, k) {
    const n = matrix.length;
    let lo = matrix[0][0];
    let hi = matrix[n - 1][n - 1];

    while (lo < hi) {
        const mid = Math.floor((lo + hi) / 2);
        const count = countLessOrEqual(matrix, mid, n);
        if (count >= k) { // in range [lo, mid]
            hi = mid;
        } else { // in range (mid, hi]
            lo = mid + 1;
        }
    }
    return lo;
};

// number of elements <= val in matrix
var countLessOrEqual = function(matrix, val, n) {
    let c = n - 1;
    let count = 0;

    for (let r = 0; r < n; r++) {
        while (matrix[r]?.[c] > val) {
            c--
        }
        count += c + 1;
    }
    return count;
};

We will implement a binary search solution. We use lo and hi as our value bounds, and mid as our test value. More specifically:

• If the number of values >= mid is >= k, then the kth smallest value must be in the range of [lo, mid].
• Otherwise, if the number of values >= mid is < k, then the kth smallest value must be in the range of (mid, hi].

Once lo and hi converges, lo will contain the correct kth smallest value.

Note that the countLessOrEqual method has runtime O(n). This is achieved using the property that matrix is sorted by rows and cols. More specifically, since all values in each row are non-decreasing, then if val is greater than the ith value of the row, val must also be greater then all values before that.