Binary Tree Maximum Path Sum
Problem
A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
The path sum of a path is the sum of the node's values in the path.
Given the root of a binary tree, return the maximum path sum of any non-empty path.
Example 1:
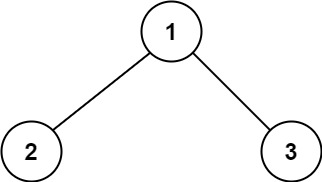
Input: root = [1,2,3] Output: 6 Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
Example 2:
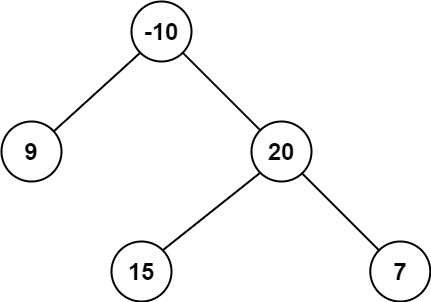
Input: root = [-10,9,20,null,null,15,7] Output: 42 Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
Constraints:
- The number of nodes in the tree is in the range
[1, 3 * 104]. -1000 <= Node.val <= 1000
Solution
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var maxPathSum = function(root) {
let maxValue = -Infinity;
const maxPath = node => {
if (!node) {
return 0;
}
const left = Math.max(maxPath(node.left), 0);
const right = Math.max(maxPath(node.right), 0);
maxValue = Math.max(left + right + node.val, maxValue);
return Math.max(left, right) + node.val;
};
maxPath(root);
return maxValue;
};
We will implement a DFS solution. We keep track of the max possible path sum in maxValue as we traverse down the tree. The max sum of any node in the tree as the root is the max sum of the left subtree plus the right subtree. Note that if the max sum is negative for either subtree, we can exclude that subtree altogether (ie. use 0 as the sum). We then update the maxValue accordingly and return the max partial path that can be used for the parent node.