Minimum Height Trees

Problem

A tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.

Given a tree of n nodes labelled from 0 to n - 1, and an array of n - 1 edges where edges[i] = [a_i, b_i] indicates that there is an undirected edge between the two nodes a_i and b_i in the tree, you can choose any node of the tree as the root. When you select a node x as the root, the result tree has height h. Among all possible rooted trees, those with minimum height (i.e. min(h)) are called minimum height trees (MHTs).

Return a list of all MHTs' root labels. You can return the answer in any order.

The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.

Example 1:

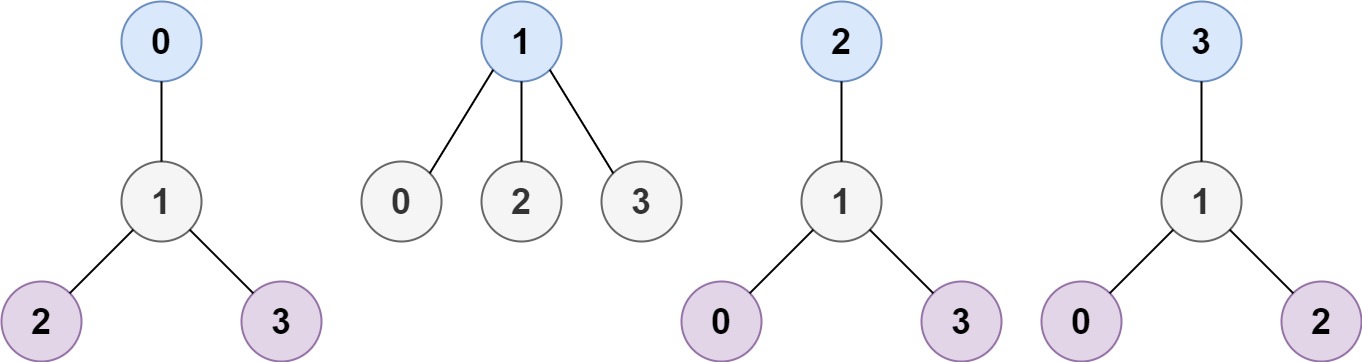
Input: n = 4, edges = [[1,0],[1,2],[1,3]]
Output: [1]
Explanation: As shown, the height of the tree is 1 when the root is the node with label 1 which is the only MHT.

Example 2:

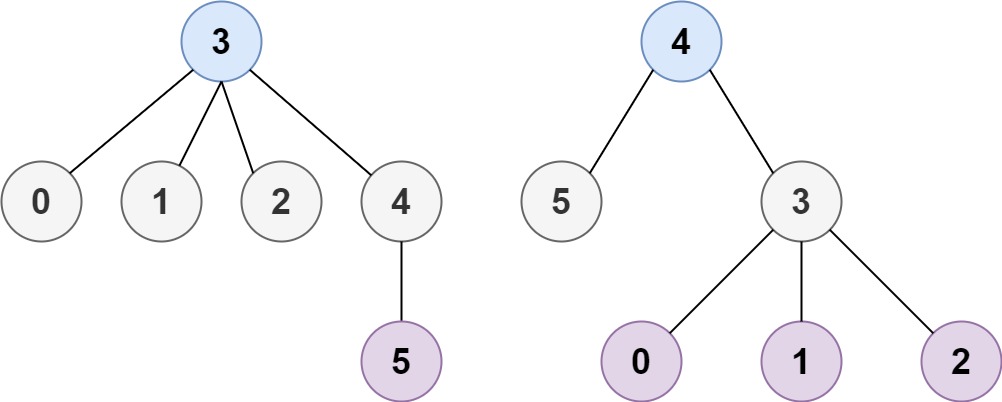
Input: n = 6, edges = [[3,0],[3,1],[3,2],[3,4],[5,4]]
Output: [3,4]

Constraints:

1 <= n <= 2 * 10⁴
edges.length == n - 1
0 <= a_i, b_i < n
a_i != b_i
All the pairs (a_i, b_i) are distinct.
The given input is guaranteed to be a tree and there will be no repeated edges.

Solution

/**
 * @param {number} n
 * @param {number[][]} edges
 * @return {number[]}
 */
var findMinHeightTrees = function(n, edges) {
    // construct adjacency graph
    const graph = Array(n).fill(null).map(() => []);
    for (const [v1, v2] of edges) {
        graph[v1].push(v2);
        graph[v2].push(v1);
    }

    // initialize queue with leaf nodes
    const queue = [];
    for (let i = 0; i < n; i++) {
        if (graph[i].length <= 1) {
            queue.push(i);
        }
    }

    // topological sort
    let nodes = n; // number of un-visited nodes
    while (nodes > 2) {
        const n = queue.length;
        nodes -= n;

        for (let j = 0; j < n; j++) {
            const leaf = queue.shift(); // leaf node
            const parent = graph[leaf].pop(); // parent of leaf node
            graph[parent].splice(graph[parent].indexOf(leaf), 1); // remove leaf from parent
            if (graph[parent].length === 1) { // parent is now leaf node
                queue.push(parent);
            }
        }
    }
    return queue;
};

We will implement a topological sort solution. More specifically, we will first create an adjacency graph graph of the tree, and use topological sort to discard the leaf nodes of graph one layer at a time. Notice that the root of a MHT is a node that is overall close to all other nodes. In other words, we want to find the centroid of the tree. Every tree can at most have two centroids (see proof below), and so we can stop our BFS when there is only two un-visited nodes remaining.

Proof

If the nodes form a chain, it is intuitive to see that the above statement holds, which can be broken into the following two cases:

If the number of nodes is even, then there would be two centroids.
If the number of nodes is odd, then there would be only one centroid.

For the rest of cases, we could prove by contradiction. Suppose that we have 3 centroids in the graph, if we remove all the non-centroid nodes in the graph, then the 3 centroids nodes must form a triangle shape, as follows:

Because these centroids are equally important to each other, and they should be equally close to each other as well. If any of the edges is missing from the triangle, then the 3 centroids would be reduced down to a single centroid.

However, the triangle shape forms a cycle which is contradicted to the condition that there is no cycle in our tree-alike graph. Similarly, for any of the cases that have more than 2 centroids, they must form a cycle among the centroids, which is contradicted to our condition.

Therefore, there cannot be more than 2 centroids in a tree-alike graph.

Problem​

Solution​

Proof​

Problem

Solution

Proof