K Closest Points to Origin

Problem

Given an array of points where points[i] = [x_i, y_i] represents a point on the X-Y plane and an integer k, return the k closest points to the origin (0, 0).

The distance between two points on the X-Y plane is the Euclidean distance (i.e., √(x₁ - x₂)² + (y₁ - y₂)²).

You may return the answer in any order. The answer is guaranteed to be unique (except for the order that it is in).

Example 1:

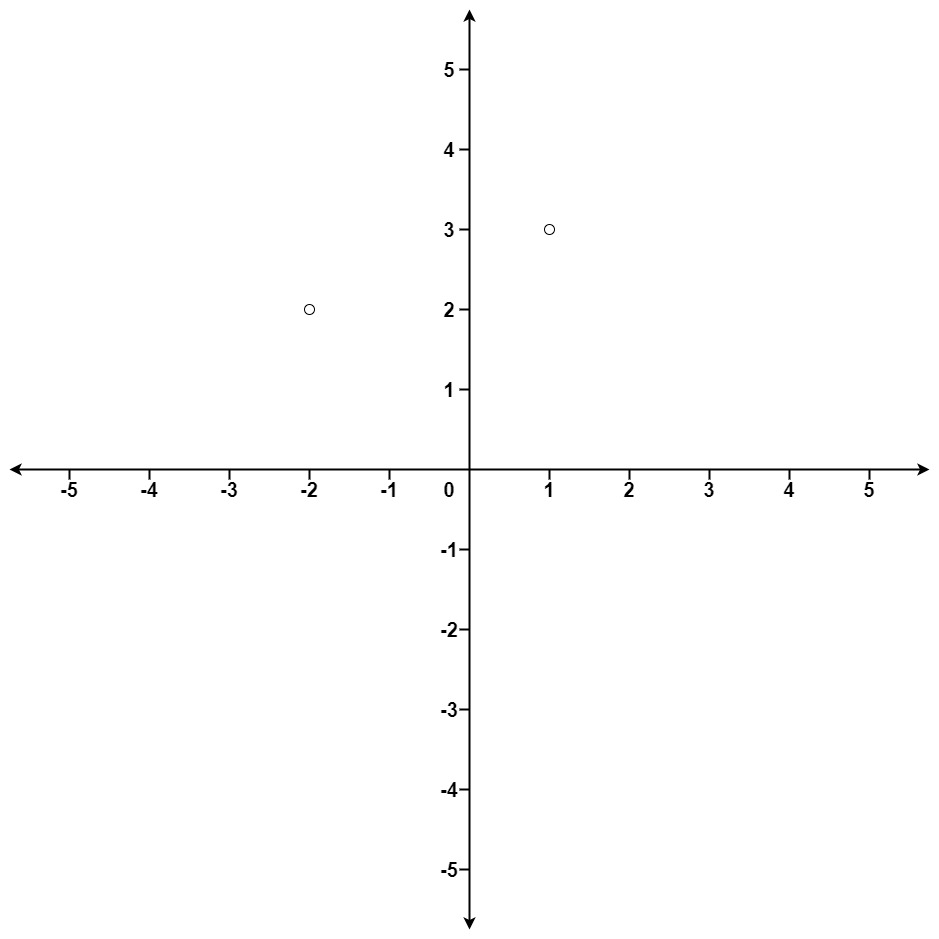
Input: points = [[1,3],[-2,2]], k = 1
Output: [[-2,2]]
Explanation:
The distance between (1, 3) and the origin is sqrt(10).
The distance between (-2, 2) and the origin is sqrt(8).
Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin.
We only want the closest k = 1 points from the origin, so the answer is just [[-2,2]].

Example 2:

Input: points = [[3,3],[5,-1],[-2,4]], k = 2
Output: [[3,3],[-2,4]]
Explanation: The answer [[-2,4],[3,3]] would also be accepted.

Constraints:

1 <= k <= points.length <= 10⁴
-10⁴ < x_i, y_i < 10⁴

Solution

/**
 * @param {number[][]} points
 * @param {number} k
 * @return {number[][]}
 */
var kClosest = function(points, k) {
    let l = 0;
    let r = points.length - 1;

    // quickselect
    while (l <= r) {
        const pivotIndex = partition(points, l, r);
        if (pivotIndex > k) { // kth before pivotIndex
            r = pivotIndex - 1;
        } else if (pivotIndex < k) { // kth after pivotIndex
            l = pivotIndex + 1;
        } else { // kth is pivotIndex
            break;
        }
    }
    return points.slice(0, k);
};

// partition all points < points[r] to left and > points[r] to right
var partition = function(points, l, r) {
    const pivotDistance = distance(points[r]);
    for (let i = l; i < r; i++) {
        if (distance(points[i]) < pivotDistance) {
            [points[i], points[l]] = [points[l], points[i]];
            l++;
        }
    }
    [points[r], points[l]] = [points[l], points[r]]; // put pivot at correct index
    return l; // index of pivot
};

// square distance of point
var distance = function(point) {
    return point[0] ** 2 + point[1] ** 2;
};

We will implement the quickselect algorithm. Recall that in quickselect, the partition function chooses a pivot p, and shuffles everything < p to the left of the array, everything > p to the right of the array (p is put between these two partitions), and returns the index of p. Since we want the k smallest values in terms of distance to the origin, if the index i returned by partition is:

> k, then the kth smallest value must be before index i.
< k, then the kth smallest value must be after index i.
= k, then points[0:k + 1] must contain the k smallest values (ie. points[i] is the kth smallest value).

Note that although quickselect has worst case runtime of O(n²), it is very fast in practice (ie. average runtime of O(n)).

Problem​

Solution​

Problem

Solution