Interval List Intersections

Problem

You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [starti, endi] and secondList[j] = [startj, endj]. Each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.

The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].

 

Example 1:

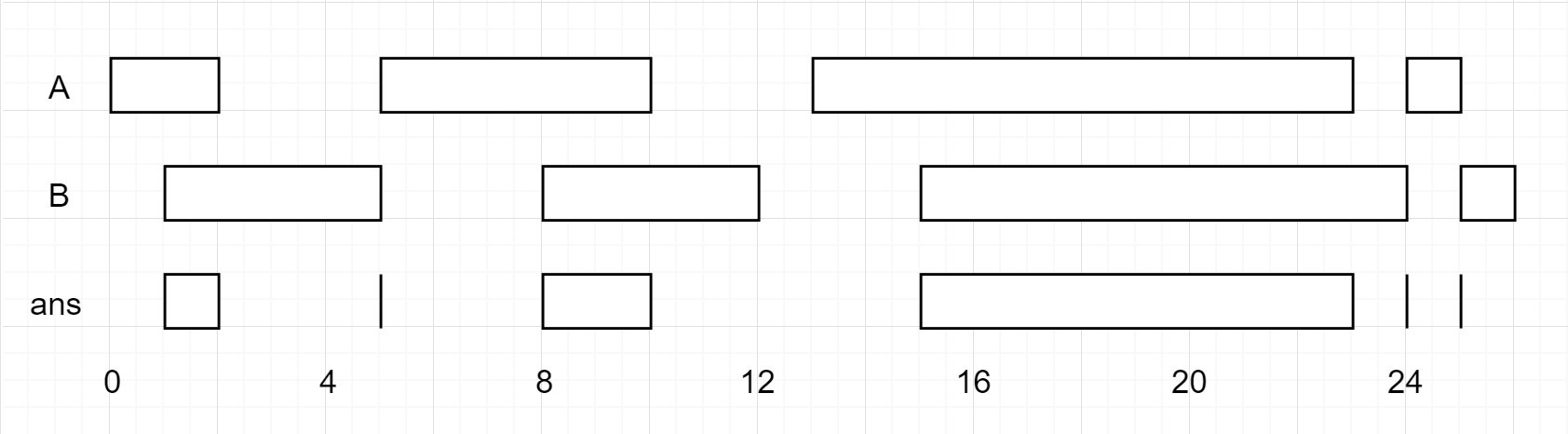
Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

Example 2:

Input: firstList = [[1,3],[5,9]], secondList = []
Output: []

 

Constraints:

• 0 <= firstList.length, secondList.length <= 1000
• firstList.length + secondList.length >= 1
• 0 <= starti < endi <= 109
• endi < starti+1
• 0 <= startj < endj <= 109
• endj < startj+1

Solution

/**
 * @param {number[][]} firstList
 * @param {number[][]} secondList
 * @return {number[][]}
 */
var intervalIntersection = function(firstList, secondList) {
    let i = 0;
    let j = 0;
    const res = [];

    while (i < firstList.length && j < secondList.length) {
        const lo = Math.max(firstList[i][0], secondList[j][0]); // max start
        const hi = Math.min(firstList[i][1], secondList[j][1]); // min end
        if (lo <= hi) { // overlap
            res.push([lo, hi]);
        }

        // remove interval with the more recent endpoint
        if (firstList[i][1] < secondList[j][1]) {
            i++;
        } else {
            j++;
        }
    }
    return res;
};

Since there are no overlaps within each list themselves, if firstList[0] has the smallest endpoint, it can only overlap with secondList[0]. Similarly, if secondList[0] has the smallest endpoint, it can only overlap with firstList[0]. Thus, after finding the overlap of the two intervals, we can discard the interval with the smallest endpoint as it cannot overlap with anything else.

Proof

Among the given intervals, consider the interval firstList[0] with the smallest endpoint (without loss of generality, assume this interval occurs in array firstList).

Then, among the intervals in array secondList, firstList[0] can only intersect one such interval in array secondList. If two intervals in secondList intersect firstList[0], then they both must overlap at the endpoint of firstList[0]; but intervals in secondList are disjoint, which is a contradiction.