Path Sum III

Problem

Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.

The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).

Example 1:

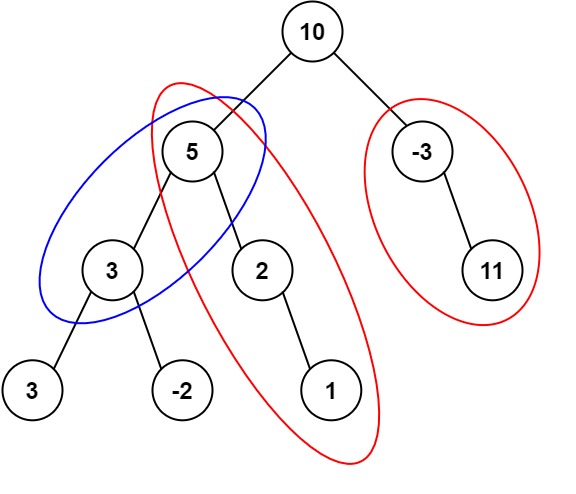
Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
Output: 3
Explanation: The paths that sum to 8 are shown.

Example 2:

Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: 3

Constraints:

The number of nodes in the tree is in the range [0, 1000].
-10⁹ <= Node.val <= 10⁹
-1000 <= targetSum <= 1000

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function(root, targetSum) {
    let res = 0;
    const map = { 0: 1 };
    const dfs = (node, pathSum) => {
        if (!node) {
            return;
        }
        pathSum += node.val;
        if ((pathSum - targetSum) in map) {
            res += map[pathSum - targetSum];
        }
        if (!(pathSum in map)) {
            map[pathSum] = 0;
        }
        map[pathSum]++;

        // recursive call
        dfs(node.left, pathSum);
        dfs(node.right, pathSum);

        map[pathSum]--;
    }
    dfs(root, 0);
    return res;
};

We will implement a DFS solution. The logic behind this solution is very similar to the Subarray Sum Equals K problem. The difference is we are working with a tree instead of an array here. Observe that we can treat the straight line path in the tree root as a linked list, which enables us to use the same logic.

Problem​

Solution​

Problem

Solution