Diameter of Binary Tree

Problem

Given the root of a binary tree, return the length of the diameter of the tree.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

Example 1:

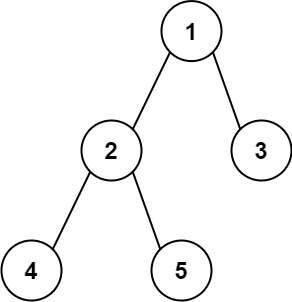
Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

Example 2:

Input: root = [1,2]
Output: 1

Constraints:

The number of nodes in the tree is in the range [1, 10⁴].
-100 <= Node.val <= 100

Solution

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var diameterOfBinaryTree = function(root) {
    let max = 0;
    const longestPath = root => {
        if (!root) {
            return 0;
        } else {
            const leftPath = longestPath(root.left);
            const rightPath = longestPath(root.right);
            max = Math.max(leftPath + rightPath, max);
            return Math.max(leftPath, rightPath) + 1;
        }
    }
    longestPath(root);
    return max;
};

We will implement a DFS solution. Observe that the max path which passes through root is the max path of the left (ie. leftPath) plus right (ie. rightPath) subtree. Thus, to find the max path that may or may not pass through root, we can check leftPath + rightPath at every node (while keeping track of the overall max path).

Problem​

Solution​

Problem

Solution