Word Search II

Problem

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

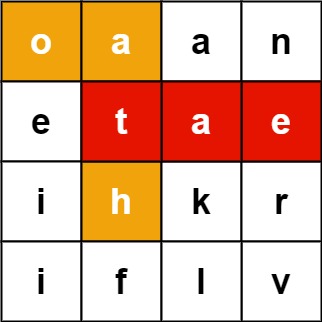
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

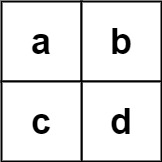
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

Constraints:

m == board.length
n == board[i].length
1 <= m, n <= 12
board[i][j] is a lowercase English letter.
1 <= words.length <= 3 * 10⁴
1 <= words[i].length <= 10
words[i] consists of lowercase English letters.
All the strings of words are unique.

Solution

/**
 * @param {character[][]} board
 * @param {string[]} words
 * @return {string[]}
 */
var findWords = function(board, words) {
    const result = [];
    const trie = new Trie();

    for (const w of words) {
        trie.insert(w);
    }

    for (let i = 0; i < board.length; i++) {
        for (let j = 0; j < board[i].length; j++) {
            dfs(board, trie.root, i, j, "", result);
        }
    }
    return result;
};

var dfs = function(board, node, row, col, path, result) {
    if (!node) { // path does not exist in trie
        return;
    }
    if (node.end) { // path exist in trie
        result.push(path);
        node.end = false;
    }
    if (board?.[row]?.[col]) { // (row, rol) is not out of range and has not been used
        const c = board[row][col];
        node = node.children[c]
        board[row][col] = null;
        dfs(board, node, row + 1, col, path + c, result);
        dfs(board, node, row - 1, col, path + c, result);
        dfs(board, node, row, col + 1, path + c, result);
        dfs(board, node, row, col - 1, path + c, result);
        board[row][col] = c;
    }
};

class Node {
    constructor() {
        this.end = false;
        this.children = {};
    }
}

class Trie {
    constructor() {
        this.root = new Node();
    }

    insert(word) {
        let r = this.root;
        for (const c of word) {
            if (!(c in r.children)) {
                r.children[c] = new Node();
            }
            r = r.children[c];
        }
        r.end = true;
    }
}

We will implement a DFS backtracking solution with a trie. First, we insert all word in words into trie. Next, we iterate through all cells of board and apply DFS method dfs at (i, j), while also keeping track of the current path and node that we are on. Once we reach any point such that node has end = true, then we know path must exist in trie and so also exist in words (note that we also set end = false to prevent the same word from being added multiple times to res). In addition, to prevent re-using the same letter cell, set the cell to null before making any recursive calls (and revert it back before returning).

Problem​

Solution​

Problem

Solution