Sort Items by Groups Respecting Dependencies

Problem

There are n items each belonging to zero or one of m groups where group[i] is the group that the i-th item belongs to and it's equal to -1 if the i-th item belongs to no group. The items and the groups are zero indexed. A group can have no item belonging to it.

Return a sorted list of the items such that:

The items that belong to the same group are next to each other in the sorted list.
There are some relations between these items where beforeItems[i] is a list containing all the items that should come before the i-th item in the sorted array (to the left of the i-th item).

Return any solution if there is more than one solution and return an empty list if there is no solution.

Example 1:

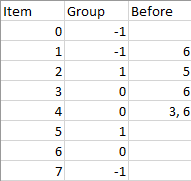
Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3,6],[],[],[]]
Output: [6,3,4,1,5,2,0,7]

Example 2:

Input: n = 8, m = 2, group = [-1,-1,1,0,0,1,0,-1], beforeItems = [[],[6],[5],[6],[3],[],[4],[]]
Output: []
Explanation: This is the same as example 1 except that 4 needs to be before 6 in the sorted list.

Constraints:

1 <= m <= n <= 3 * 10⁴
group.length == beforeItems.length == n
-1 <= group[i] <= m - 1
0 <= beforeItems[i].length <= n - 1
0 <= beforeItems[i][j] <= n - 1
i != beforeItems[i][j]
beforeItems[i] does not contain duplicates elements.

Solution

/**
 * @param {number} n
 * @param {number} m
 * @param {number[]} group
 * @param {number[][]} beforeItems
 * @return {number[]}
 */
var sortItems = function(n, m, group, beforeItems) {
    // create new group for each item without a group
    for (let i = 0; i < n; i++) {
        if (group[i] === -1) {
            group[i] = m;
            m++;
        }
    }

    // create two adjacency graphs (one for item and one for group)
    const graphItem = Array(n).fill(null).map(() => []);
    const indegreeItem = Array(n).fill(0);

    const graphGroup = Array(m).fill(null).map(() => []);
    const indegreeGroup = Array(m).fill(0);

    for (let i = 0; i < n; i++) {
        const bItems = beforeItems[i];
        for (const u of bItems) { // u must come before i
            graphItem[u].push(i);
            indegreeItem[i]++;

            if (group[u] !== group[i]) { // group[u] must come before group[i]
                graphGroup[group[u]].push(group[i]);
                indegreeGroup[group[i]]++;
            }
        }
    }

    // topological sort both graphItem and graphGroup
    const itemSort = topSort(graphItem, indegreeItem);
    const groupSort = topSort(graphGroup, indegreeGroup);

    // topological sort does not exist
    if (itemSort.length !== n || groupSort.length !== m) {
        return [];
    }

    // sort each item relative to their own group
    const bucket = Array(m).fill(null).map(() => []);
    for (const u of itemSort) {
        bucket[group[u]].push(u);
    }

    // sort each group
    const res = [];
    for (const group of groupSort) {
        res.push(...bucket[group]);
    }
    return res;
};

// topological sort graph with indegree
var topSort = function(graph, indegree) {
    const res = [];
    const queue = indegree.reduce((acc, cur, i) => {
        if (!cur) {
            res.push(i);
            acc.push(i);
        }
        return acc;
    }, []);

    while (queue.length) {
        const u = queue.pop();
        for (const v of graph[u]) {
            indegree[v]--;
            if (!indegree[v]) {
                res.push(v);
                queue.push(v);
            }
        }
    }
    return res;
};

We will implement a topological sort solution. We first create two adjacency graphs, graphItem and graphGroup, based on the ordering of items and the ordering of groups respectively (we also create a new group for each item that does not have a group to avoid dealing with edge cases). Next, we simply find the topological sort itemSort and groupSort of graphItem and graphGroup respectively. If a topological sort doesn't exist for either one of the graphs, it must mean no possible ordering exists, otherwise an ordering must exist. Finally, we sort each item relative to their own group using the ordering of itemSort, and then put each group in their correct position using the ordering of groupSort.

Problem​

Solution​

Problem

Solution