N-Queens

Problem

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

Example 1:

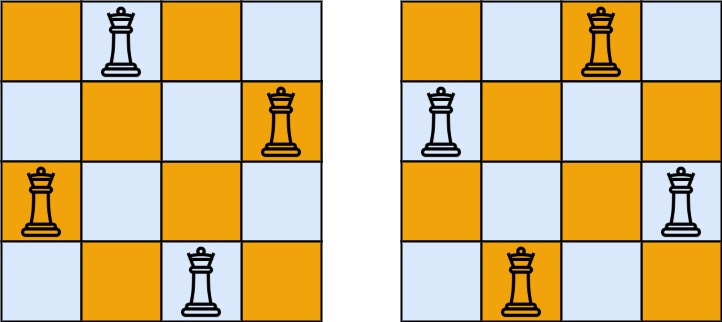
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Example 2:

Input: n = 1
Output: [["Q"]]

Constraints:

1 <= n <= 9

Solution

/**
 * @param {number} n
 * @return {string[][]}
 */
var solveNQueens = function(n) {
    const res = [];
    backtrack(n, res, [], 0);
    return res;
};

var backtrack = function(n, res, queens, r) {
    if (queens.length === n) {
        res.push(queens.map(queen => {
            const col = queen[1];
            return ".".repeat(col) + "Q" + ".".repeat(n - col - 1);
        }));
    } else {
        for (let c = 0; c < n; c++) { // n possible cols
            if (isValid(queens, r, c)) {
                queens.push([r, c]);
                backtrack(n, res, queens, r + 1);
                queens.pop();
            }
        }
    }
};

// check if placing queen at (r, c) is valid
var isValid = function(queens, r, c) {
    for (const [r2, c2] of queens) {
        const slope = Math.abs((r2 - r) / (c2 - c));
        if (r2 === r || c2 === c || slope === 1) {
            return false;
        }
    }
    return true;
};

We will implement a backtracking (DFS) solution. Our method backtrack places the queen row by row before backtracking to the previous row and trying the next col (ie. the loop tries all cols and the recursive call tries all rows). The parameter queens contains (r, c) value of queens that we have already placed on the board; it is also used in isValid to check the validity of a coordinate as well as construct the solution that is put into res.

Problem​

Solution​

Problem

Solution